
You may specify the value of a free variable at any point in the equation, but only the first domain specification will be recognized. Piecewise functions may reference free variables (a, b, c, etc.), but all pieces must use the same value for each variable. Note that x 1 is less than 0, so we use the first piece and write f (1) 0.

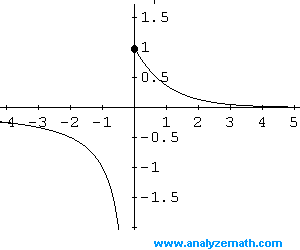
You just have to select the correct piece. Solution Because each piece of the function in (6) is constant, evaluation of the function is pretty easy. You can define piecewise functions of x, y, or theta (polar coordinates), but you may not mix functions of different variables in the same equation. Sketch the graph of the piecewise function f. The graph of a piecewise-defined function may contain internal endcaps if adjacent pieces do not evaluate to the same result at the transition points. This means that you must specify domains for pieces that abut one another using interval notation so the program can tell which function defines the value for the transition point between the pieces. The domains are not required to span the entire real number line, but they must not overlap. You must specify a domain for each piece, and order the pieces by increasing domain values. Enter all of the pieces of the equation on the same line, separated by semicolons ( ). You can enter Cartesian and polar equations as single-valued piecewise-defined functions. This idea is better illustrated in the following example.Graphmatica Help - Piecewise-Defined Functions Then the domain of the piecewise function is the concatenation of these domains, and the range of the piecewise function is the contatenation of the ranges of the functions on their corresponding domains. To identify the domain and range of a piecewise function, we recall that a piecewise function is defined by different functions each with corresponding domains. In the first region, \(x \ge 3\text\) as shown in Figure144. Half-Angle and Angle Sum and Difference Identities.
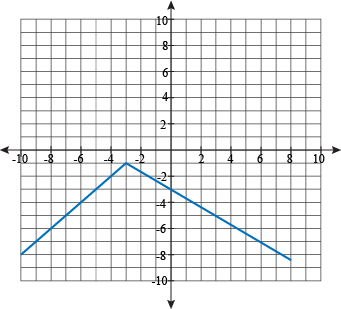
General method: The trick to this is knowing that expressions involving, <, >.Introduction to Trigonometric Identities Using a calculator to create the graph of a piecewise-defined function (TI 83).Modeling with Generalized Sinusoidal Functions.Relationships Between Trigonometric Functions.Find and position integers and other rational numbers on a horizontal or vertical number line diagram find and position pairs of integers and other rational numbers on a. To graph the linear function, we can use two points to connect the line. First I created the piecewise function function x pieceWise (t) if t > 0 & t <3 x exp (-t) else x 0 endif then called and plot it here x linspace (-1,5,1000) y pieceWise (x) plot (x,y) but the output is always 0 any hint would be very helpful. For all intervals of x other than when it is equal to 0, f (x) 2x (which is a linear function). Using the graph, determine its domain and range. Keywords: piecewise function graph piecwise linear function Background Tutorials. Graph the piecewise function shown below. III College Trigonometry 1 Introduction to Trigonometry This tutorial shows you the entire process for graphing a piecewise linear function. Short-Run Behavior of Rational Functions.


 0 kommentar(er)
0 kommentar(er)
